Réseaux électriques
Un réseau électrique est un ensemble de producteurs (ex. centrales) et de consommateurs (ex. usines, villes) interconnectés par des lignes et des commutateurs. Lorsqu’un commutateur est activé, l’ensemble des sources connectées seront alimentées par l’ensemble des producteurs connectés. L’appel de puissance des consommateurs est répartie équitablement sur l’ensemble des producteurs. Le choix de l’activation de tout les commutateurs du réseau est donc cruciale, car c’est de elle que dépend la répartition de la charge électrique sur l’ensemble des lignes. Si cette charge est trop importante pour une ligne, on s’expose à des pannes en cascade. Enfin certaines stratégies d’activation sont meilleurs que d’autres car elles peuvent conduire à une meilleure répartition de la charge sur les producteurs.
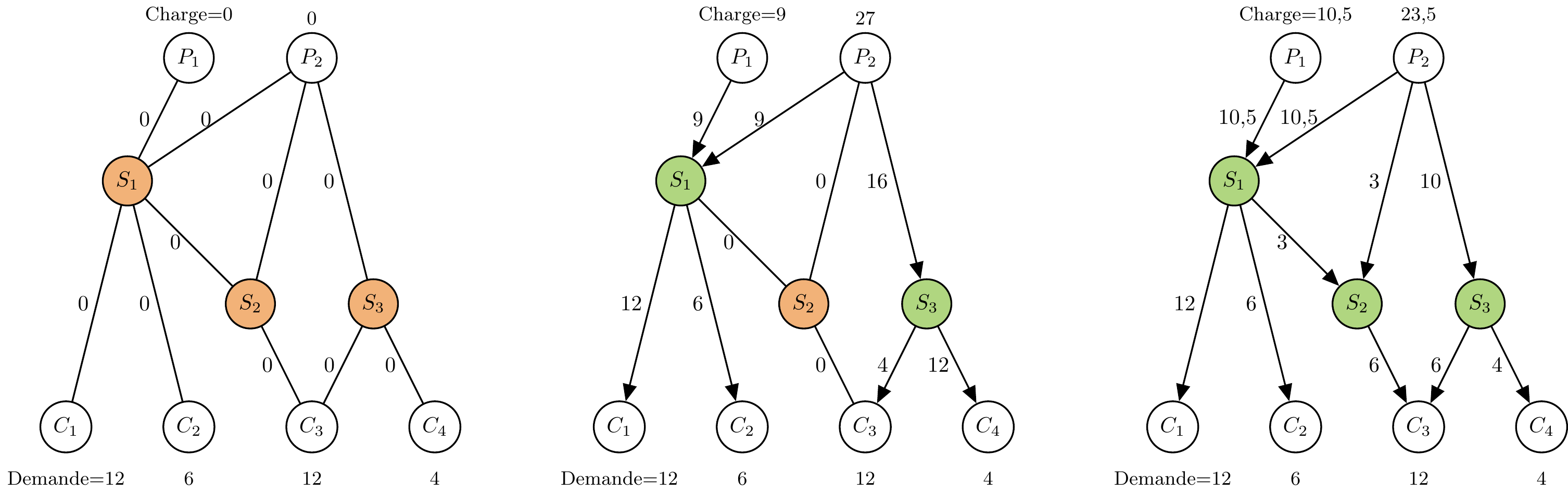
Figure 1: Exemple d’activations possibles et de conséquence sur le flot.
Nous avons proposé une modélisation pour ce problème à l’aide de flots particuliers car il doivent respecter la contrainte de repartition équitable de la charge des consommateurs sur les producteurs. Nous avons prouvé que le problème de savoir si une activation des commutateurs est possible sans enfreindre les contraintes du réseau est NP-complet. Nous avons proposé un algorithme polynomial dans le cas où le réseau de commutateurs est un anneau [1] ou un arbre [2,3].
Redécouverte de réseaux
Dans les réseaux, la connaissance des équipements, de leurs emplacements et de leurs fonctions est une des informations les plus importantes pour leur maintenance et leur évolution. Dans de nombreux contextes, la topologie d’un réseau a été perdue, contient des erreurs, est incomplète ou synoptique. C’est le cas des réseaux de gaz naturel ou d’eau des quartiers, des réseaux électriques des anciens bâtiments et usines, et plus récemment des data centers aux infrastructures complexes et aux modifications régulières de la topologie. La question est donc de pouvoir retrouver la topologie d’un réseau uniquement à partir de mesures sur les équipements accessibles.
Une solution consiste à faire des mesures de corrélations physiques sur quelques arêtes accessibles afin d’estimer la probabilité d’incidence entre chaque paire d’arêtes. Lorsque les mesures sont correctes, les corrélations fournissent des informations sur la matrice d’adjacence du linéaire \(L\) de la topologie (c’est-à-dire le graphique qui représente les adjacences entre les bords de la topologie). La multiplication de telles mesures permet de déduire le linegraph entier \(L\) ce qui suffit à retrouver la topologie correspondante. Malheureusement, les mesures sont souvent bruitées et donc le graphe inféré \(L\) n’est pas un linéaire. Une correction doit être appliquée, pour trouver le linegraph le plus proche de \(L\), en termes de distance d’édition : ajouter ou supprimer le nombre minimum de sommets ou d’arêtes à \(L\) pour qu’il devienne un linegraph. Par exemple, ajouter une arête à \(L\) signifie qu’une mesure de corrélation entre deux arêtes de la topologie est un faux négatif, et ajouter un sommet à \(L\) signifie qu’une arête est cachée et non accessible.
Nous avons prouvé que le problème est NP-Complet lorsque seule l’addition est autorisée [4]. La question reste ouverte lorsque l’ajout et la suppression sont simultanément autorisés.
Réseau tout optique
Les spécificités de la lumière rendent la gestion des réseaux tout optique assez particulière, et les problématiques d’optimisation qui en découlent également. Les thèses de David Poulain [5] et Vincent Reinhard [6] ont été l’occasion d’abborder ces sujets.
Avec le projet de réseau très haut débit CARRIOCAS (40 Gbps par longueur d’ondes), nous nous sommmes intéressé à des algorithmes pour le traitement des demandes de multicasts. En effet, dans le réseau, un nombre fini et fixé de nœuds (que nous appelons nœuds diffusants) sont capables de dupliquer les flux de données. Dans un arbre multicast, seul ces nœuds peuvent avoir plusieurs fils, ce qui introduit une contrainte forte sur la construction de ces arbres. Nous développons donc de nouvelles méthodes pour traiter les demandes de multicast en respectant cette contrainte, afin de minimiser la bande passante nécessaire à ces communications [7–9].
Dans le contexte des réseaux métropolitains, optiques transparents à faible consommation d’énergie en anneaux, nous avons étudié des problèmes de dimensionnement. En particulier, ces réseaux disposent de multiplexers (Packet Optical Add-Drop Multiplexer, POADM) permettant d’améliorer les performances tout en diminuant la consommation d’énergie. Le nombre de ces équipements est variable dans chaque noeud et détermine les performances du noeud mais aussi son coût de déploiement. Nous avons proposé des solutions de dimensionnement ppour à la fois de garantir les performances du réseau tout en minimisant le coût de déploiement de celui-ci [10,11].
Réseau interdomaine
L’étude du réseau interdomaine Internet et de nouveaux algorithmes de routage pour éviter les congestion a été l’objet de ma thèse [12] soutenu en 2007. Les travaux que nous avons proposé repose sur le structuration hiérarchique du réseau au niveau inter-domaine. Cette hiérarchie provient des contrats commerciaux qui lient les opérateurs de réseaux entre eux et conditionnent les routes empruntées par les paquets dans Internet.
Nous avons proposé un mécanisme, basé sur cette hiérarchie, pour détecter les routes non-congestionnées et adapter les routes [13]. L’évaluation de performence de cet algorithme a nécessité la généreration un grand nombre de topologies aléatoires ayant des propriétés proche du réseau interdomaine. Les générateurs existants ne prenant pas en compte le découpage hiérarchique des domaines en Tier, nous avons proposé notre générateur aléatoire, aSHIIP [14–17].
Une paranthèse, une étude au niveau intra-domaine, et l’introduction d’un algorithme pour gérer la micro-mobilité au niveau d’IP [18].