Similarité Moléculaire
Un plan de synthèse est, pour une molécule donnée, une séquence de réactions permettant de la produire à partir de molécules commercialisées ou facilement synthétisables. Pour aider à la conception d’un plan de synthèse pour une nouvelle molécule il est nécessaire d’analyser les très grandes bases de données de réactions moléculaires existantes afin d’identifier et d’adapter un plan de synthèse d’une molécule existante proche. Il faut donc être capable de mesurer la proximité de deux molécules et en particulier des cycles qui les composent et qui formet leur ossature.
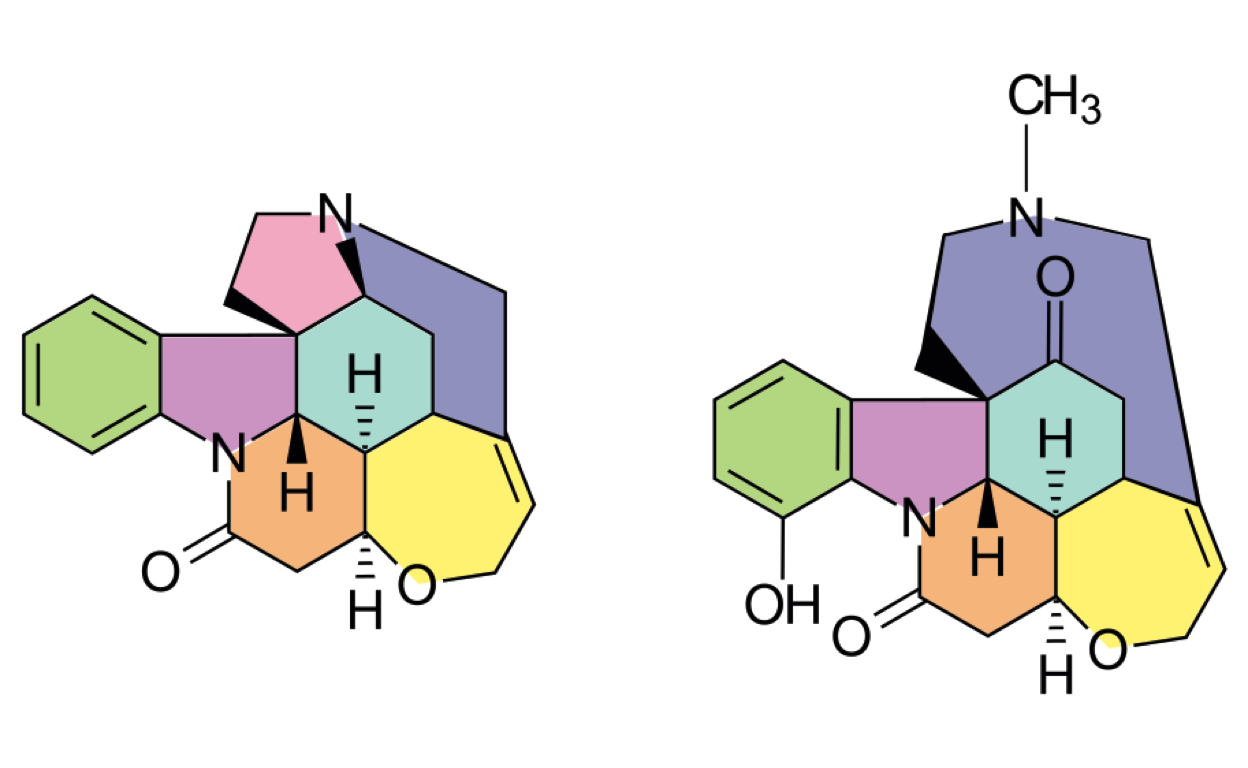
Figure 1: Deux molécules structurellement proches : Strychnine et Vomicine
Ce travail a été l’objet de la thèse de Stefi Nouhelo [1]. Nous y introduisons une représentation structurelle des molécules appelée graphe de cycles [2]. Cette représentation est basée sur les cycles du graphe moléculaire et leurs interconnexions. Cette représentation est canonique et permet de définir une mesure de similarité entre les structures de molécules et nécessite un temps de calcul raisonnable. Nos études montrent qu’elle est plus adaptée pour les travaux sur les plans de synthèse que les autres mesures de similarité existantes.
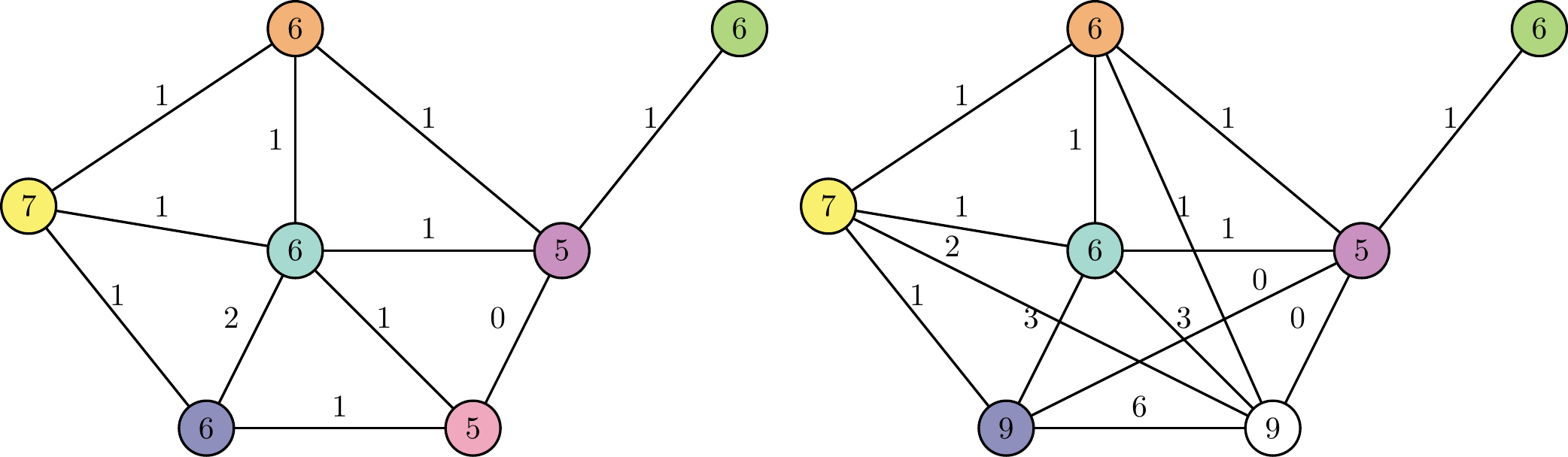
Figure 2: Graphes de cycles associés aux molécules ci-dessus
À partir des graphes des cycles, nous proposons une classification des réactions en fonction des effets sur la structure des molécules. Il s’agit de la première étape pour la prédiction des plans de synthèse.
Dynamique Moléculaire
L’analyse de la dynamique moléculaire est un sujet fondamental en chimie, en particulier l’étude de la formation et de la dissolution des liaisons hydrogène au fil du temps. La dynamique de ces liaisons crée et rompt des cycles qui sont cruciaux pour la structure des molécules. Le défi de l’analyse des cycles est double : il existe un nombre exponentiel de cycles, et certains cycles sont très proches.
Nous introduisons une approche basée sur les graphes utilisant des bases de cycles minimum pour aider à l’analyse de la dynamique moléculaire. Étant donné un ensemble de graphes représentant une trajectoire de molécule, nous déterminons, pour chaque graphe, une base de cycles minimum et construisons un graphe de cycles qui représente les cycles des bases minimales et leurs interactions. Ensuite, nous agrégeons toutes les informations de ces graphes de cycles dans un polygraphe. Chaque sommet du polygraphe représente une classe de cycles apparaissant dans différentes bases minimales et jouant des rôles équivalents dans la trajectoire [3].
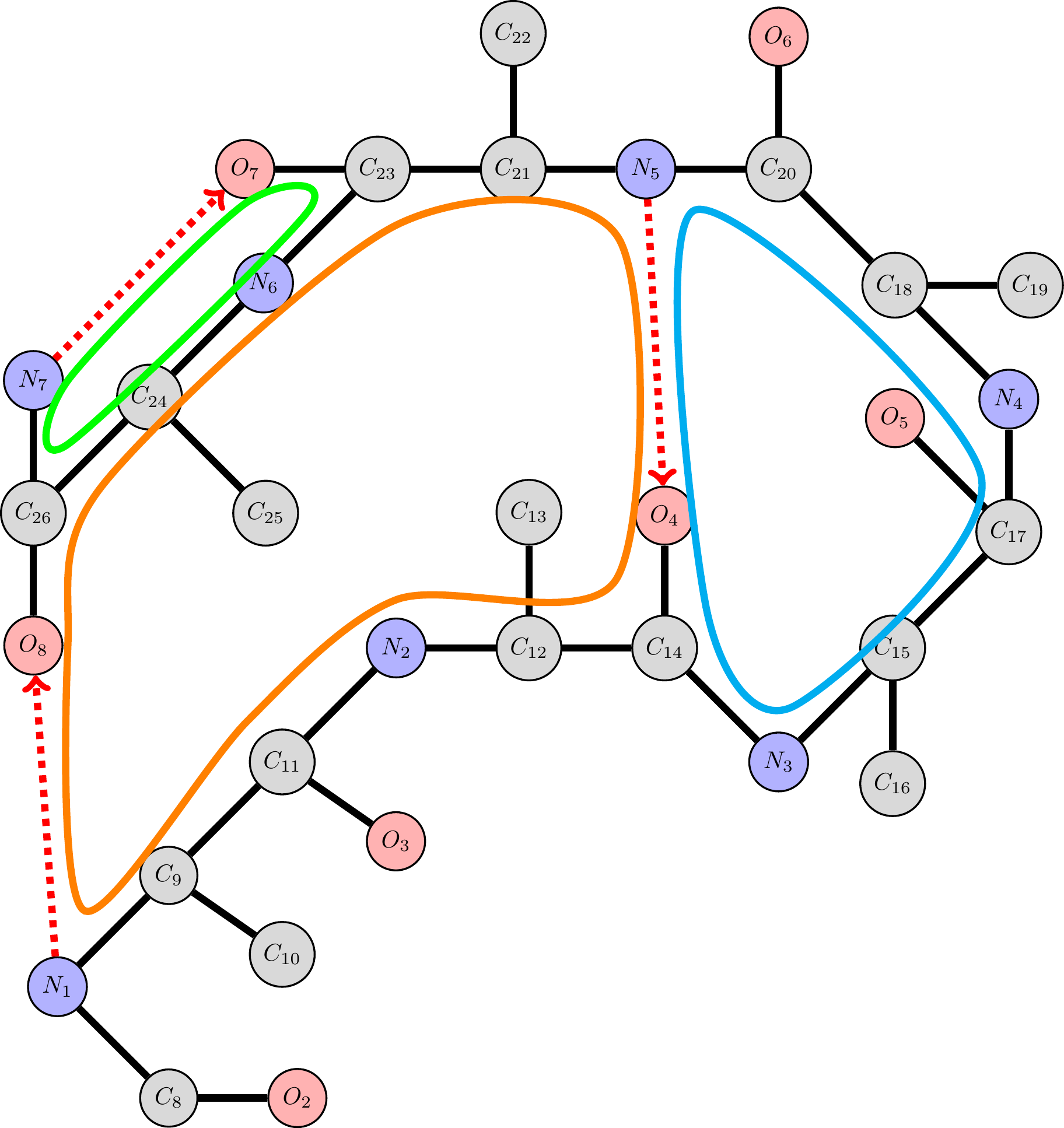
Figure 3: Exemple du peptide Zala6 avec ces liaisons hydrogène en pointillé et les cycles structurant la forme 3D.
Réseau de Petri
Un enjeu aujourd’hui est de réaliser des plans de synthèse qui privilégie certaines réactions plutôt que d’autres. À partir de base de données rescensant les réactions connues, il faut alors trouver le plan de synthèse optimisant un critère écologique ou économique.
Les réseaux de Petri sont traditionnelement utilisés pour représenter les séries de réactions présentes dans un plan de synthèse. Le soucis est que ces réseaux ne prennent pas en compte de pondération permettant d’introduire le critère à optimiser. Nous avons donc étendu les réseaux de Petri afin d’introduire une notion de poids sur les transitions [5].
Nous avons montré que le problème de trouver le plan de synthèse dans un tel réseau est un problème EXPSPACE-complet et qu’il n’existe pas d’algorithme d’approximation polynomial y compris lorsque le degré sortant des noeuds du réseau est limité à 2. Nous avons enfin montré qu’une version contrainte du problème, dans laquelle le nombre de transitions actionnées est limité, est PSPACE-complet. Le problème paramétré par le nombre de transitions actionnées tombe dans XP mais reste inapproximable.