Aborescence de Steiner
Étant donnés un graphe orienté \(G=(V,A)\) avec \(n\) noeuds, \(m\) arcs, une racine \(r\in V\) et \(V'\subseteq V\) un ensemble de \(k\) terminaux, une arborescence de Steiner de poids minimum est une arborescence enraciné en \(r\), sous-graphe de \(G\), contenant tous les terminaux et tel que le nombre d’arcs qui la compose est mininmum. Ce problème est NP-complet, on sait qu’il n’existe pas d’algorithme d’approximation à rapport constant, on sait également qu’il existe des \(k^\epsilon\)-approximations mais jusqu’à présent l’existance ou non d’une \(\log{k}\)-approximation est une question ouverte.
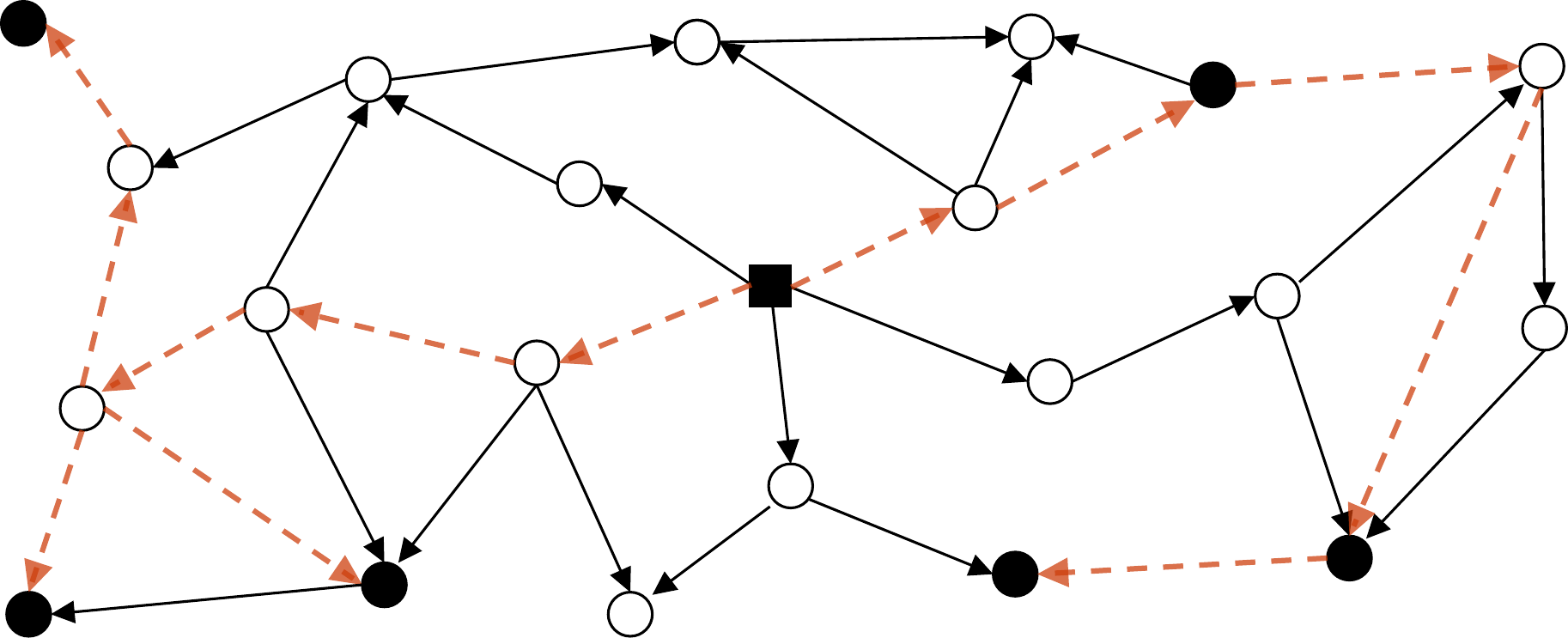
Figure 1: Exemple d’instance d’arborescence de Steiner
Ce sujet a été l’objet de la thèse de Dimitri Watel [1] que j’ai co-encadré de 2011 a 2014 avec Cédric Bentz et Dominique Barth. Cette thèse a abouti à la création de deux algorithmes basés sur un principe innovant, une forme de flots très particuliers. Ils fournissent respectivement des \(k\) et \(\sqrt{k}\)-approximations avec des complexités polynomiales inférieures à l’existant [2,3].
Nous avons introduit une variante de problème de l’arborescence en limitant le nombre \(d\) de noeuds ayant un degré supérieur à deux : les noeuds de branchement. Les principaux résultats pour ce problème, DSTLD, sont qu’il est NP-complet et appartient à la classe XP vis à vis du paramètre \(d\). Nous avons, entre autres, proposé un algorithme FPT vis à vis de \(k\) et de \(d\) qui nous a permis de proposer le premier algorithme, pour l’arborescence de Steiner qui soit à la fois FPT vis à vis \(k\) en temps et en espace. Nous avons également pu déduire une nouvelle \(\lceil \frac{k-1}{d} \rceil\)-approximation pour le problème de l’arborescence de Steiner [4–8].
Hypercube latin
Un hypercube latin \(H\) de taille \(n\) et de dimension \(d\) est un ensemble de \(n\) points, \(h_i \in [1\ldots n]^d\), tel qu’aucun couple de points ne partagent une même coordonnée pour chaque dimension. On s’interesse en particulier aux hypercubes latins maximin, c’est à dire, ceux maximisant la distance minimum entre tout couple de points, la distance de séparation. La norme considérée pour calculer la distance est le plus souvent \(L_1\) (Manhattan), \(L_2\) (euclidienne) ou \(L_\infty\) (Tchebychev).
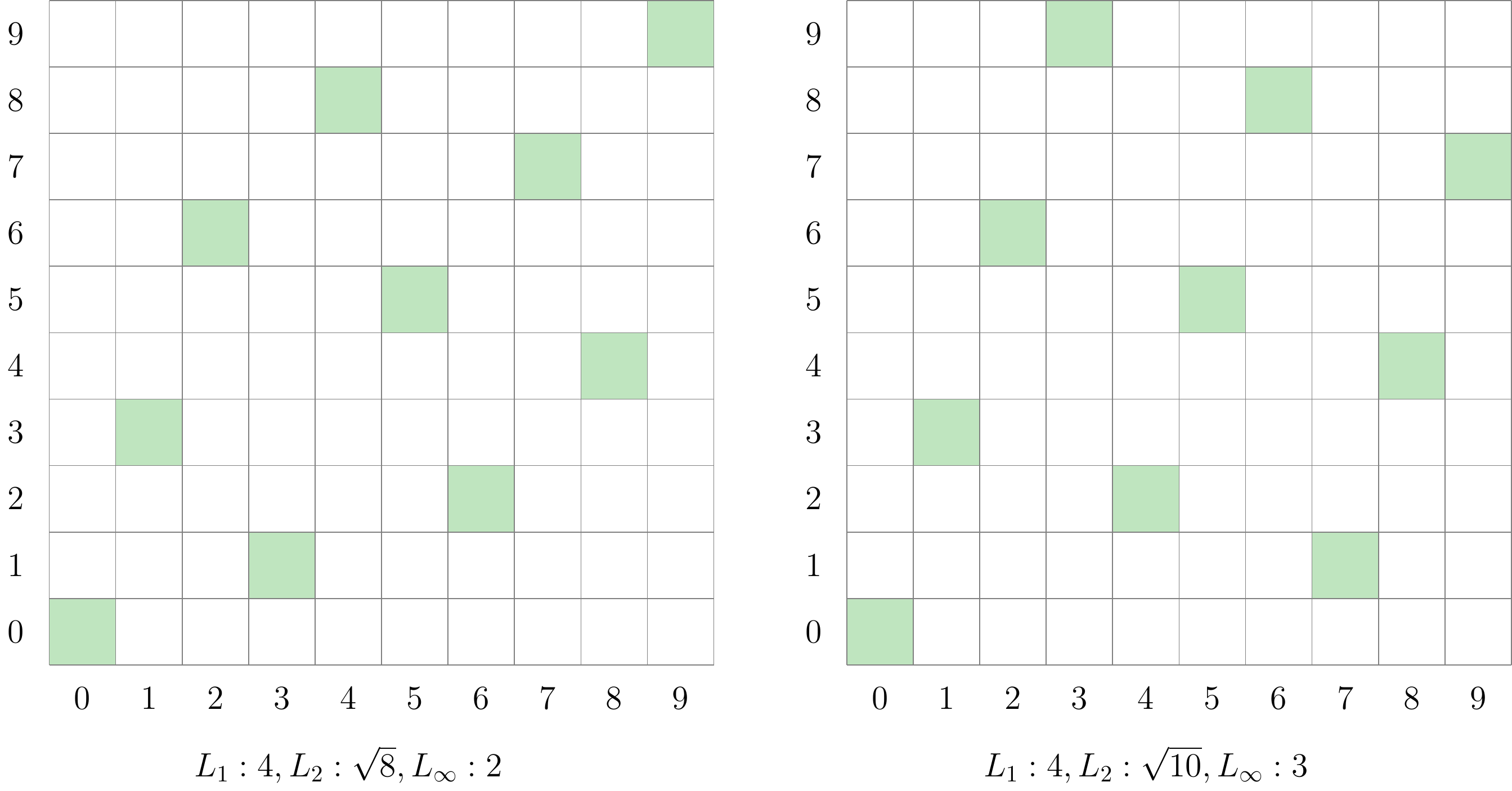
Figure 2: Exemples d’hypercubes maximins et distance de séparations associées
Les hypercubes latins ont été l’objet de la thèse de Kaourintin Le Guiban [9]. À ce jour, les seuls algorithmes de constructions d’hypercubes ont des complexités exponentielles en \(n^d\). Nous avons introduit des bornes sur la distanece de séparation et nous avons proposé un premier algorithme d’approximation pour le \(k=2\) et \(L_\infty\) [10].
Une extension possible de ce problème est de compléter un hypercube partiel, toujours en maximisant la distance de séparation. Nous avons montré que le problème est NP-complet dès \(d=2\), quelque soit la norme et des résultats d’inapproximabilité [11].
| Dimension | Norme | Complexité | Approximation |
|---|---|---|---|
| \(d>2\) | Toute norme | NP-complet | pas d’\(\epsilon\)-approximation \(\forall \epsilon > 0\) |
| \(d=2\) | \(L_i, i\in \mathbb{N}\) | NP-complet | inconnu |
| \(d=2\) | \(L_\infty\) | NP-complet | pas d’\(\epsilon\)-approximation \(\forall \epsilon > 2/3\) |
Nous avons également proposé des algorithmes heuristiques pour les deux problèmes (construction et complétion) basé sur le recuit simulé.
Empaquetage
Dans le problème classique de Bin Packing, l’enjeu est de placer un ensemble \(E\) d’éléments entiers dans un nombre minimum de sac de taille \(B \in \mathbb{N}\).
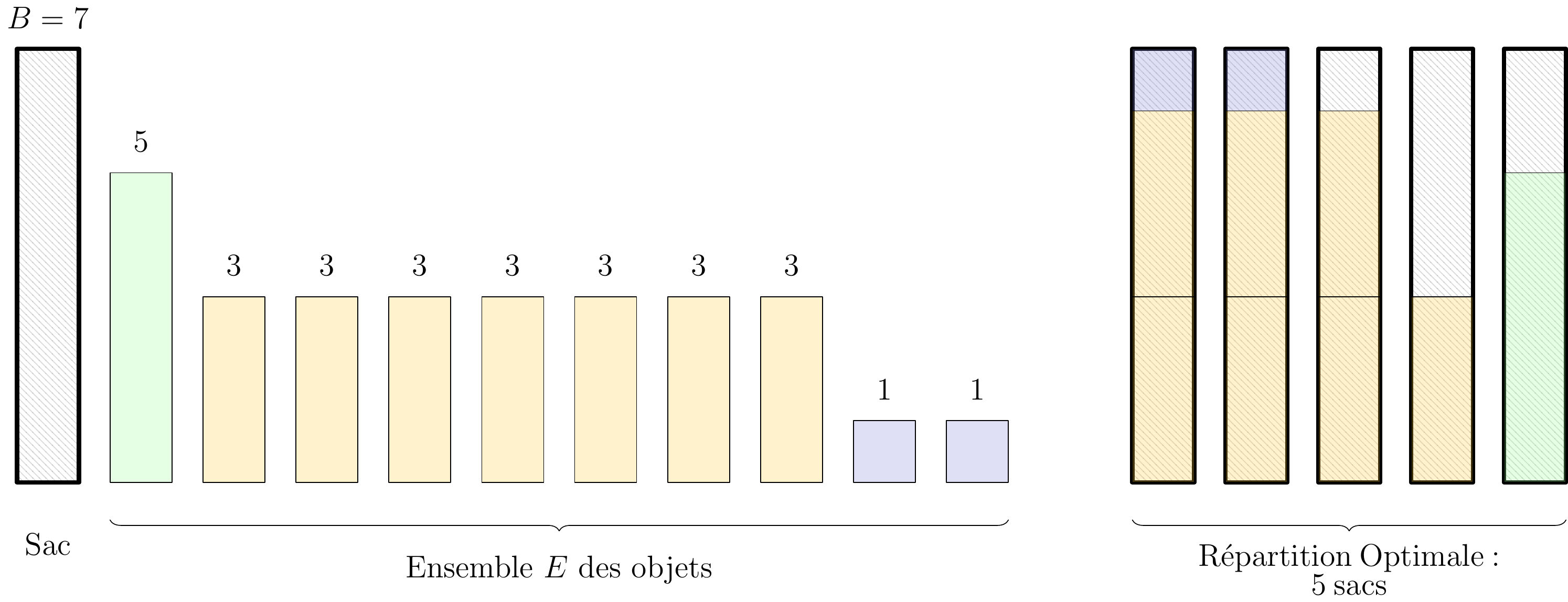
Figure 3: Exemple d’instance de Bin Packing
Nous considérons une variante du Bin Packing Problem traitant d’objets fragmentables, qui peuvent être coupés et placer dans plusieurs sacs. On connait dès lors le nombre de sacs pour stocker les objets. L’objectif est de touts les placer en les fractionnant en un nombre minimum de fragments.
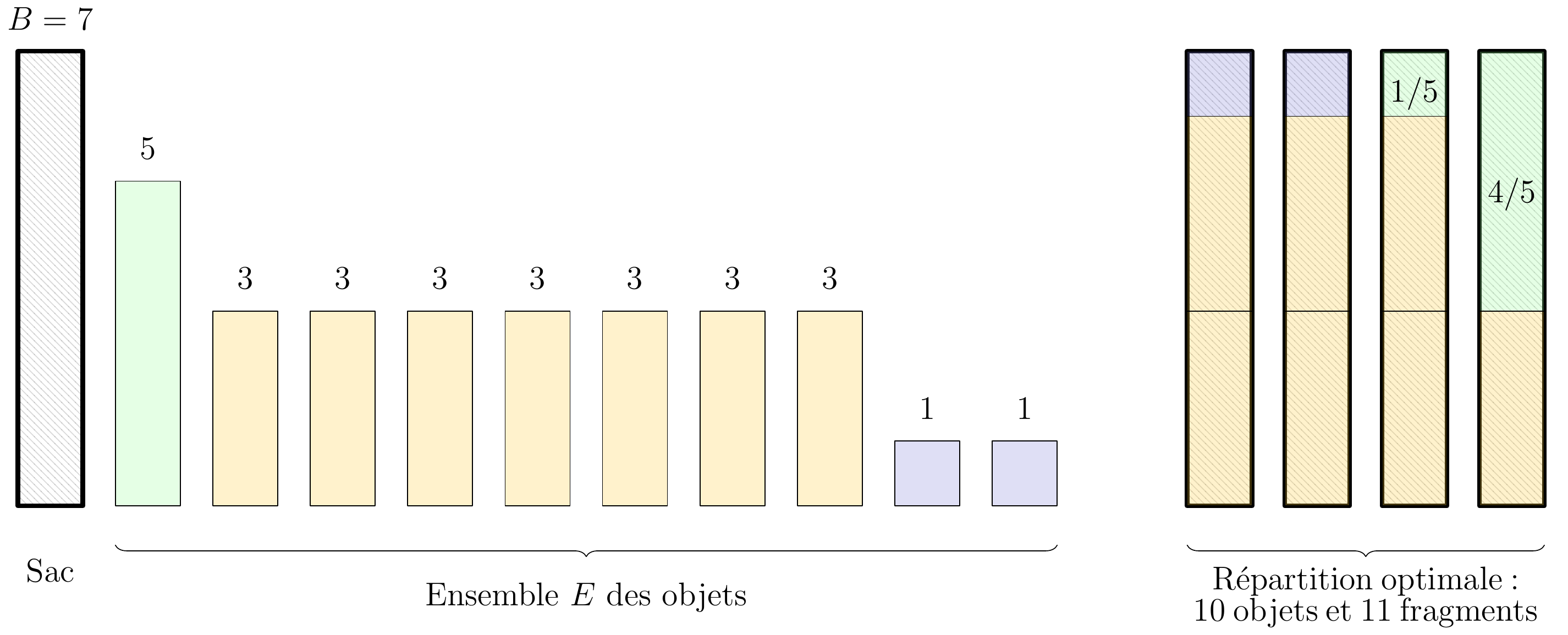
Figure 4: Exemple d’instance de Bin Packing avec fragmentations
Nous avons introduit cette variante, montré sa NP-complétude et fourni une \(6/5\)-approximation pour le cas particulier dans lequel tous les sacs ont les mêmes capacités [12].